Machine Learning notes for Andrew Ng on Coursera

These are my personal notes for the "Machine Learning" Coursera course given by Andrew Ng (ex Google Brain). I want to learn more and understand this domain better.

Week 1 Topic 1 - Supervised vs Unsupervised machine learning

Machine learning as the field of study that gives computers the ability to learn without being explicitly programmed

Two main types of machine learning:

1. supervised learning - the data comes with both x input and y output

• regression: a type of supervised learning: to predict a number from infinitely many possible numbers 
• classification: another type of supervised learning: has a small finite number of outputs (categories) predicted

2. unsupervised learning - the data comes with inputs x but not y, algorithm has to find structure/pattern in the data

• clustering algorithm: takes data and groups into categories
• anomaly detection:
• dimensionality reduction:

Supervised learning

Regression supervised machine learning 

Refers to algorithms that learn x to y, or aka input to output mappings. 

key characteristic:you give your learning algorithm examples to learn from. That includes the right answers, whereby right answer, is correct label y for input x

• e.g. given email as input, the output is spam or not spam?
• e.g. given english text as input, the output is german
• e.g. input is image & radar info, output is position of objects nearby (self driving)
• e.g. given sq feet of house, what is predicted sales price?

In these examples we would provide data as examples so it can lean e.g. emails which are and are not spam

Classification supervised machine learning

Example given was tumor screening app to answer if tumor is benin or malignant. 

Can plot data set of size of tumor to risk of malignant on x and y axis. Also included persons age as another data input or thickness of turmor, uniformity and more data

Predicted categories could be numeric or if photo is a cat or dog

Unsupervised learning

Called unsupervised because we're not trying to supervise the algorithm. Instead, we asked the algorithm to figure out all on its own what's interesting. 

"clustering algorithm" a kind of unsupervised algorithm - clusters data groups together e.g. google new example clustered similar news stories in a feed

  e.g. based on dna characteristics, could group people into ctagegories

  Useful for dealing with large data and drawing conclusions

"anomaly detection"

"dimensionality reduction"

The "Jupyter Notebook" is an in browser environment to test ideas. It's the same tool devs use in large companies now.

• has 2 types of cells: markdown and code
• to run py code, can either be in cell and hit Shift + Enter or click run icon

Week 1 Topic 2 - Regression Modal (supervised learning)

Linear Regression Model. 

Just means fitting a straight line to your data. Widely used.

• e.g. Graph of house sq footage to house price

Linear Regression Model an example of a regression model. There are others

Could also use a table/matrix to represent the data

Data input is called a Training set. 

Notation callouts

• x often used to denote input
• y often used to denote output aka "target", true value
•  m number of training examples (i.e. x y pairs)
• (x,y) a single training example and x to i and y to i denote the x y values for the ith training row

For house data one training example could be a house of 2104 sq ft which sold for $400k. In which case x = 2104 and y = 400. (x,y) = (2104, 400)

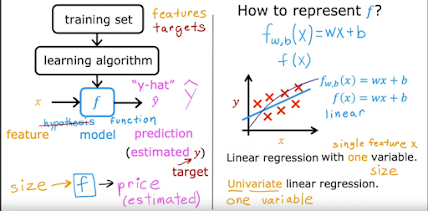
To train the model you feed the training set (both input & output) to your learning algorithm. Then the algorithm will produce some function "f" i.e. f(x) -> y hat   (y hat, caret over y)

The function f is known as "the model"

In the house sale example, your model f, given the size, outputs the price which is the estimator, that is the prediction of what the true price will be

  fw,b(x) = wx + b    or simplified f(x) = wx + b

𝑓𝑤,𝑏(𝑥(𝑖))=𝑤𝑥(𝑖)+𝑏

The values choosen for w and b are numbers and will determine the value of "y hat" based on input x

• note: w is weight and b is bias; w and b are parameters and are used to improve the model

This simple house sale example is known as "Linear regression with one variable" aka "Univariate (one va) linear regression" (the one variable is the house sq feet size)

Linear regression builds a model which establishes a relationship between features and targets

• in the example, the feature was house size and the target was house price
• for simple linear regression, the model has two parameters 𝑤 and 𝑏 whose values are 'fit' using training data.
• once a model's parameters have been determined, the model can be used to make predictions on novel data.

Cost function 

We try to find values for w and b to get "yhat" as close to actual y as possible. A Cost function measures how well the model function fits the training data

we say "error" = yhat - y

cost function J(w,b) = sum all training data(yhat^i - y^i )sqr    divided by 1/2m

you want J(w,b) as small as possible

which is: 

𝐽(𝑤,𝑏)=12𝑚∑𝑖=0𝑚−1(𝑓𝑤,𝑏(𝑥(𝑖))−𝑦(𝑖))2

this is known as the "squared error cost function" which is the mostly commonly used

example when w = 1  

• left side chart represents training set when x is 1, 2 and 3
• now try with w = 1 (and b is 0)
• to calculate cost J of J(w)
• you get all zeros because f(x^i) is same as y and this J(w) is zeros
• e.g. J(1) = 0

example: when w = 0.5

example when w = 0

So for different values of w you can plot what J(w) will be. 

You want to choose w to minimize J(w)

In this graph when w = 1 then J(w) = 0. And w = 1 is the best w to choose

Goal of linear regression is the find the parameters w or w and b that results in the smallest possible value for cost function J

Q: When does the model fit the data relatively well, compared to other choices for parameter w?

A: When the cost $J$ is at or near a minimum.

To summarize

fyi here's an example of a not so good choice of values for w and b

Visualizing the cost function

Contour plots are 

a convenient way to visualize the 3D cost function J,

Contour plots are 3d surface on a 2d plot

Consider this plot for w and b. It's a pretty good fit to the trining data chart top left. Notice it targets the smallest contour in the contour plot chat. w and b intersect near smallest contour.

Contrast it with this chart which is not a good fit. Notice w and b plotted on the contour chart are away from the smallest contour

Gradient descent

Is an algorithm to help find optimal values for w and b to minimize the cost function. There could be many parameters (not just 1 w), w1...wn. Gradient descent works for multiples too.

Gradient descent works by making incremental steps to get to the lowest value for w and b (aka "local minima"). When the data is complex there could be multiple local minima

Here's the algorithm, notice both a new w and b are calculated. The α alpha is the "learning rate" and its a value used in the equation, the bigger it is the bigger the gradient step.

The learning rate $𝛼$ is always a positive number, so if you take W minus a positive number, you end up with a new value for W that is smaller

Also called out is the importance of using current value of w in b's calculation; "simultaneous update"

Examples of 2 w (x axis) values, one larger, one smaller

fyi when $\frac{\mathrm{\partial }𝐽(𝑤,𝑏)}{\mathrm{\partial }𝑤}$ is a negative number (less than zero), $w$ increases after one update step

Learning rate

When the  α alpha "learning rate" is too small then steps are small and it takes a long time to get to the minimum. i.e. Gradient Descent will work but its slow

When the  α alpha "learning rate" is too large then you may miss the minimum cost because the steps are too large i.e. May overshoot and never reach the minimum.

So choosing the right value for learning rate is important.

What if you're already at the local minima for J?

Then w = w - α * 0
Simplified w = w    

As nears a local minina, the derivative becomes smaller. Which means the Update steps become smaller.

Gradient descent for linear regression

This image recaps the functions including Gradient descent:

Recall, you can have more than 1 local minimum

When you're using a squared error cost function with linear regression, the cost function does not and will never have multiple local minima. It has a single global minimum because of this bowl-shape. 

The technical term for this is that this cost function is a convex function

When you implement gradient descent on a convex function, one nice property is that so long as you're learning rate is chosen appropriately, it will always converge to the global minimum.

"Batch Gradient descent" each step of gradient descent uses all the training examples.

There are other variants of Gradient descent which are not batch.

$\mathrm{𝐽<span\; style="font-family:\; KaTeX\_Math;\; font-size:\; 1.21em;\; font-style:\; italic;\; white-space:\; nowrap;">J</span><span\; face=""Source\; Sans\; Pro",\; Arial,\; sans-serif"\; style="-webkit-font-smoothing:\; antialiased;\; box-sizing:\; inherit;\; font-size:\; 16px;"><span\; style="-webkit-font-smoothing:\; antialiased;\; box-sizing:\; inherit;">\; is\; at\; or\; near\; a\; minimum.</span></span>}$

Week 2 Multiple Features

In previous we had a single "feature", x, the size in feet which gave us y. But in reality for pricing we'd use many features besides size such as # bedrooms, # bathrooms, age of home etc.

features go from x1 to xn

n is total number of features

We can see the data represented as a table and 1 row of all the values is a "row vector" (one column of all values in column is a "column vector" (a vector is just a list of numbers)

You can identify a cell row 2 col 3 as x superscript 2 subscript 3

$1_{(4)}^{}$ is the first feature (first column in the table) of the fourth training example (fourth row in the table) which is the value 852 (row 4, col 1)

Our old linear regression formula with 1 feature (x) was: fw,b(x) = wx + b 

But that need to change to support many x's now like so:
  fw,b(x) = w1x1 + w2x2 + w3x3 + w4x4 + b 

this can be rewritten as

notice shorthand multiplying two vectors of w and x (dot product)

This is known as "multiple linear regression" because have multiple features.

The dot product is a mainstay of Linear Algebra and NumPy. This is an operation used extensively in this course and should be well understood. The dot product is shown below.

The dot product multiplies the values in two vectors element-wise and then sums the result. Vector dot product requires the dimensions of the two vectors to be the same.

Vectorization 

Makes ML code shorter and simpler by using libraries.

In Linear algebra count starts at 1, but python starts at 0

numpy (numerical python) is most commonly used python library and used a lot in ML

can write py code to loop over and multiply vectors/arrays w and x

    x=0

    for i in range(a.shape[0]):

        x = x + a[i] * b[i]

    return x

but numpy provides a vectorization fn, np.dot which takes vectors: 

   f = np.dot(w,x) + b

...which runs faster by hardware parallelization optimization (gpu) GPU's and modern CPU's implement Single Instruction, Multiple Data (SIMD) pipelines allowing multiple operations to be issued in parallel. This is critical in Machine Learning where the data sets are often very large.

Matrices are 2 dimensional arrays. 

Typically m is number rows and n columns. 

Indexed by 2D index e.g X[0,5]   1st row, 5th column

Gradient descent for multiple linear regression

Contrast old notations (left side) with new (vectors)

Gradient descent with one feature (left) and multiple (right)

Side note: "Normal equation" is an alternative to Gradient Descent

• only for linear regression
• solve for w,b without iterations
• slow when #features > 10k

Gradient Descent is often the best choice.